Análisis estadístico de datos

Caso

Queremos saber en qué medida influyen el sexo, la edad y la altura de una persona en su peso. En este caso, la variable dependiente sería el peso y las variables independientes, sexo, edad y altura.

Descripción de la técnica aplicable

Una posible técnica a aplicar pasaría por realizar una regresión lineal. El resultado final de la aplicación de esta técnica vendría a ser una ecuación con un aspecto similar a la siguiente:

Peso (kilos)=0,07342*Altura(centímetros)+0,2314*Edad (años)-0,5672*Sexo-2,348

Tipos de variables

La variable dependiente será cuantitativa, las variables independientes pueden ser cuantitativas o cualitativas. En caso de trabajar con variables cualitativas (el sexo, por ejemplo), será necesario recodificarlas. Por ejemplo, en el caso anterior se podría recodificar el sexo de la siguiente forma:

• Hombre=0
• Mujer=1

Justificación teórica

La regresión lineal se ajusta basándose en el método de los mínimos cuadrados. En esencia, lo que se busca dados un conjunto de pares ordenados: variable independiente, variable dependiente, y una familia de funciones, aquella que se aproxime mejor a los datos (un "mejor ajuste").

Este ajuste intenta minimizar la suma de cuadrados de las diferencias en las ordenadas entre los puntos generados por la función elegida y los correspondientes valores en los datos.

El método de los mínimos cuadrados requiere que los errores de cada medida estén distribuidos de forma aleatoria.

Interpretación de resultados

Debemos analizar el coeficiente de determinación R² . Este coeficiente indica en qué medida los valores reales del peso se ajustan a la ecuación que hemos calculado y oscila entre 0 y 1. En sentido estricto, es el cuadrado del coeficiente de correlación lineal de Pearson. De cara a saber si nuestra ecuación se ajusta a los valores observados, R² =1, implica una relación lineal exacta. Por contra, si R²=0, quiere decir que no existe relación lineal.

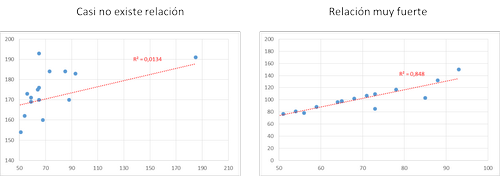
En la imagen siguiente se muestran dos rectas de regresión (tono rojo) que tratan de ajustarse a una serie de valores. La primera de ellas apenas “explica” estos valores, por el contrario la segunda se ajusta muy bien a los mismos.

Observaciones

• Es importante tener en cuenta que con esta técnica se busca saber si existe una relación lineal entre variable dependiente e independientes. Podría darse el caso de que dicha relación fuera de carácter no lineal. De ser así, habría que aplicar otras técnicas de análisis..
• Nos podemos dar por satisfechos si R²>0,65. Lo normal es que no se llegue a este valor.
• Si utilizamos un paquete estadístico (SPSS o similar) para calcular la regresión, conviene meter en los estadísticos la prueba de Durbin-Watson, que indica la autocorrelación de variables. El valor de la prueba oscila entre 0 y 4. Si es 2, no hay autocorrelación. Cuando se aleja de este valor, existe autocorrelación, por lo que deberíamos revisar las variables, dado que algunas de ellas están correladas entre sí.
Para poder crear un modelo de regresión lineal, es necesario que se cumpla con los siguientes supuestos:
• Relación lineal entre variables.
• Los errores en la medición de las variables explicativas son independientes entre sí.
• Los errores tienen varianza constante.
• Los errores tienen una esperanza matemática igual a cero (los errores de una misma magnitud y distinto signo son equiprobables).

Descarga PDF