Caso
Queremos comprobar si la cantidad de folletos publicitarios repartidos en varios códigos postales guarda relación con las ventas.
Descripción de la técnica aplicable
El coeficiente de correlación lineal nos arroja un valor que nos dice si existe relación entre dos variables de tipo cuantitativo.
En este caso, tenemos las variables:
- Número de folletos publicitarios repartidos.
- Ventas en un determinado periodo.
Tipos de variables
Dos de tipo cuantitativo.
Justificación teórica
El coeficiente de correlación entre dos variables aleatorias X e Y es el cociente:
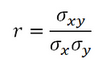
Donde:
-
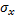 : es la desviación típica de la variable x
: es la desviación típica de la variable x
-
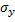 : es la desviación típica de la variable y
: es la desviación típica de la variable y
-
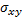 : es la covarianza entre las variables x e y
: es la covarianza entre las variables x e y
Interpretación de resultados
El valor del índice de correlación varía en el intervalo [-1, +1]:
- Si r = 1, existe una correlación positiva perfecta. El índice indica una dependencia total entre las dos variables denominada relación directa: cuando una de ellas aumenta, la otra también lo hace en proporción constante.
- Si 0 < r < 1, existe una correlación positiva.
- Si r = 0, no existe relación lineal.
- Si -1 < r < 0, existe una correlación negativa.
- Si r = -1, existe una correlación negativa perfecta. El índice indica una dependencia total entre las dos variables llamada relación inversa: cuando una de ellas aumenta, la otra disminuye en proporción constante.
Supongamos que el valor de la correlación es 0,56. Esto quiere decir que la campaña publicitaria ha funcionado ya que existe una correlación positiva significativa entre ambas variables.
Truco
- Diremos que existe relación si r, en valor absoluto es mayor que 0,35, en caso contrario, la relación es muy débil.
- Si r = 0, no existe relación lineal. Pero esto no necesariamente implica que las variables son independientes: pueden existir todavía relaciones no lineales entre las dos variables. En este caso hay que recurrir al coeficiente de Cochran.
Descarga PDF